Индикаторы риска

1. Альфа индекс (альфа Йенсена)
2. Бета индекс
3. Коэффициент Шарпа
4. Среднее квадратическое отклонение



1. Альфа индекс (альфа Йенсена).

Показатель эффективности инвестиционного портфеля; определяет разницу между фактической доходностью фонда и его ожидаемой доходностью при заданном уровне риска (измеряемого с помощью показателя бета (beta)). Положительное значение альфы указывает на то, что фонд показал лучшие результаты, чем можно было бы предполагать, судя по его бете. Напротив, отрицательное значение альфы говорит о том, что доходность фонда является недостаточно высокой в сравнении с ожиданиями, основанными на бете. Этот показатель эффективности базируется на модели CAPM (Capital Assets Pricing Model), демонстрирующей соотношение ожидаемого риска и дохода и основанной на допущении, что инвесторы хотят получать более высокий доход при повышенном риске. Согласно указанной концепции, ожидаемая доходность ценной бумаги зависит от ее чувствительности к колебаниям индекса широкого рынка. Скорректированная по риску эффективность фонда может быть выражена уравнением линейной регрессии, соотносящим действительную избыточную доходность данного фонда с действительной избыточной доходностью общерыночного портфеля.

Из уравнения регрессии:

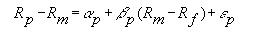
где:
Rp – доходность портфеля фонда
Rm – доходность рыночного индекса
Rf – доходность безрискового инструмента
ep – случайная погрешность
Rm - Rf – избыточная доходность портфеля фонда
можно найти значение альфы Йенсена:

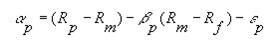
Некоторые инвесторы рассматривают альфу Йенсена как показатель качества работы менеджера фонда, т.е. меру добавленной или вычтенной стоимости портфеля, обусловленной работой менеджера. Однако при помощи альфы не всегда можно дать точную оценку деятельности менеджера. В некоторых случаях отрицательное значение альфы может быть следствием расходов, отраженных в результатах фонда, но не представленных в результатах соответствующего индекса. Альфа зависит от точности расчета беты: если инвестор принимает бету как окончательную меру риска, то положительное значение альфы будет итоговым индикатором позитивных результатов фонда. Однако следует иметь в виду, что значение беты зависит и от другого статистического показателя, известного как R-квадрат (R-squared).
^наверх



2. Бета индекс.

Используется для оценки степени чувствительности фонда к колебаниям рынка. Измеряет систематический, или недиверсифицируемый, риск, присущий портфелю фонда. Обычно рассчитывают бету фонда, используя то же самое уравнение регрессии, которое используется для расчета альфы (регрессия избыточной доходности фонда против избыточной доходности индекса). Таким образом, для расчета беты измеряется разница между избыточной доходностью взаимного фонда по отношению к доходности казначейских векселей и избыточной доходностью индекса широкого рынка.

Доходность фондов, инвестирующих в акции, сопоставляется с доходностью индекса S&P 500, а доходность облигационных фондов – с индексом облигаций, рассчитываемым фирмой Lehman Brothers (LEH), - Lehman Brothers Aggregate Bond Index. Этот подход несколько отличается от других методов расчета беты, которые основаны на регрессии показателей общей доходности (без вычитания доходности безрисковых инструментов).

Из уравнения регрессии:

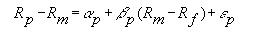
где:
Rp – доходность портфеля фонда
Rm – доходность рыночного индекса
Rf –доходность безрискового инструмента ep – случайная погрешность
Rm - Rf – избыточная доходность портфеля фонда
можно найти значение беты:

Показатель беты широкого рынка принимается за 1,00. Соответственно, если бета фонда равна 1,15, это означает, что в случае роста широкого рынка, избыточная доходность фонда, в исторической перспективе, на 15% превышает доходность базового индекса, а в случае падения рынка результаты фонда оказываются на 15% ниже (при условии, что другие факторы остаются неизменными). Напротив, бета 0,85 указывает на то, что результаты фонда на 15% ниже результатов широкого рынка в периоды его роста и на 15% выше в периоды падения. В то же время низкое значение беты не обязательно говорит о низком уровне волатильности фонда; скорее, оно свидетельствует о низком риске, связанном с рыночными колебаниями. Если фонд специализируется на активах, слабо коррелирующих с индексом S&P 500, то его бета не будет представлять особо большого значения для инвесторов.
^наверх



3. Коэффициент Шарпа.

Этот коэффициент, формула расчета которого разработана лауреатом Нобелевской премии Биллом Шарпом (Bill Sharpe), показывает соотношение доходности и риска, точнее, он измеряет избыточность доходности портфеля на единицу риска. Коэффициент определяется как отношение среднегодовой избыточной доходности фонда по сравнению с доходностью “безрисковых” инвестиционных инструментов (казначейских векселей со сроком погашения 90 дней) к стандартному отклонению (изменчивости) этой избыточной доходности фонда, отражающая ее изменение от одного периода (например, месяца) к другому. Чем больше коэффициент Шарпа, тем выше историческая доходность фонда на единицу риска.

Коэффициент Шарпа рассчитывается по следующей формуле:

где:
Rp – доходность портфеля фонда
Rf - доходность безрискового инструмента
Rp - Rf- средняя избыточная доходность портфеля относительно доходности безрискового инструмента
σ(Rp - Rf) - среднее квадратическое отклонение избыточной доходности портфеля фонда

Для расчета коэффициента Шарпа для фондов обычно используют среднемесячную доходность 90-дневных казначейских векселей (за 36-месячный период) и среднемесячную доходность фонда за тот же период. Разница между показателем общей среднемесячной доходности фонда и среднемесячной доходности казначейских векселей представляет собой избыточную доходность фонда. Затем рассчитывается избыточная доходность фонда в годовом исчислении (путем умножения месячного результата на 12), а затем это значение делится на стандартное отклонение избыточной доходности фонда в годовом исчислении. В отличие от коэффициента альфа, коэффициент Шарпа оценивает другой аспект эффективности портфеля фонда, так как при его расчете используется иной показатель риска (стандартное отклонение, а не бета как при расчете коэффициента альфа).
^наверх



4. Среднее квадратическое отклонение

Статистический показатель разброса результатов взаимного фонда. Если фонд имеет высокое значение среднего квадратического отклонения, разброс его результатов очень велик, т.е. фонд потенциально очень волатилен. Низкое значение среднего квадратического отклонения показывает, что доходность фонда является почти постоянной величиной. Среднегодовое среднее квадратическое отклонение фонда, указываемое в обзорах, рассчитывается на основе статистических данных о доходности фонда за 36 месяцев.

По определению, в течение приблизительно 68% времени общая доходность любого фонда не должна отклоняться от средней доходности в сторону увеличения или уменьшения на величину, превышающую среднее квадратическое отклонение. Кроме того, в течение приблизительно 95% времени общая доходность фонда не должна отклоняться в любую сторону от его средней доходности на величину, превышающую двукратное значение среднего квадратического отклонения. Соответствие этим параметрам означает, что показатели доходности фонда попадают на типичную колоколообразную кривую нормального распределения вероятностей. В любом случае, чем больше среднее квадратическое отклонение, тем выше волатильность фонда. Недостаток этого статистического показателя состоит в том, что значение среднего квадратического отклонения иногда может быть равно нулю, отражая последовательно низкие результаты фонда.
^наверх